

- Example of impulsive force how to#
- Example of impulsive force series#
- Example of impulsive force free#
How to Decrease the Impulsive Force…………? Decrease the time of impact How to Increase the Impulsive Force…………?ġ1 An impulsive force needs to be reducedġ. F = Impulsive force, t = time, m = mass, v & u = velocityįalling down the glass to the floor Hitting a nail using hammer Kicking a football Collision of cars Striking a tennis ball Etc. Change of momentum Time of impact The shorter the time of impact, the bigger the impulsive force. Impulsive force is defined as the rate of change of momentum of an object in a collision or explosion. Impulsive Force is a large force that acts over a short period of time during collisions or explosions. Equations: Ft = mv-mu ……….? F = m a Ft = mv-mu F = Impulsive force, a = acceleration, t = time, m = mass, v & u = velocityĨ The shorter the time of impact, the bigger the impulsive force. The product of impulsive force (F) and the time of impact (t).

So whether you call it a force acting over a period of time or an impulse is entirely up to you, the problem at hand and convention.6 Impulse is defined as change in momentum of an object.įt = mv-mu Change of momentum F = Impulsive force, t = time, m = mass, v & u = velocityħ Ft = mv-mu Ft = mv-mu Impulse Equations: ……….? F = m a In fact in solving such a problem the word momentum is probably never used?
Example of impulsive force series#
It certainly does not make the problem easier to solve by saying that the mass is subjected to a whole series of delta functions as it falls although in a sense you do exactly that when an integration is performed.
Example of impulsive force free#
Now in the case of free fall the evaluation of the impulse is relatively easy in that the force, $mg$, does not change with time and one tends not to use the word impulse in such a situation. However Mathematics via the delta function allows you to apply an impulse to a body which changes the momentum of the body in a time period which is not of interest to you. There is no point in speculating about a force that acts for no time as that force does nothing. So it is not a force which acts for no time, it is a force which acts fro a time much less that the time scale under consideration and as far as the change in momentum of the falling body is concerned it the force, which happens to be constant in this case) times the time over which the facts which is important. So in such an example a certain amount of momentum is being transferred to a body in next to no time. In collision problems it is convenient to say that the force acts over a very small period of time but what is important to me is not the actual magnitude of the force or the actual time over which it acts but the area under the force against time graph which is the impulse.Ī mathematically convenient way of doing this is to write the impulse in terms of the delta function $10 \ \delta(0)$ Ns as the delta function has an area of one. You will note that the impulse is the area under a force against time graph. The only difference is that now the body reaches $10$ m/s half a second after the force was first applied.Īs you can see from the graphs the impulse in the same and so is the final state, speed is $10$ m/s but as the time over which the force acts decreases so the time taken to reach the final state.
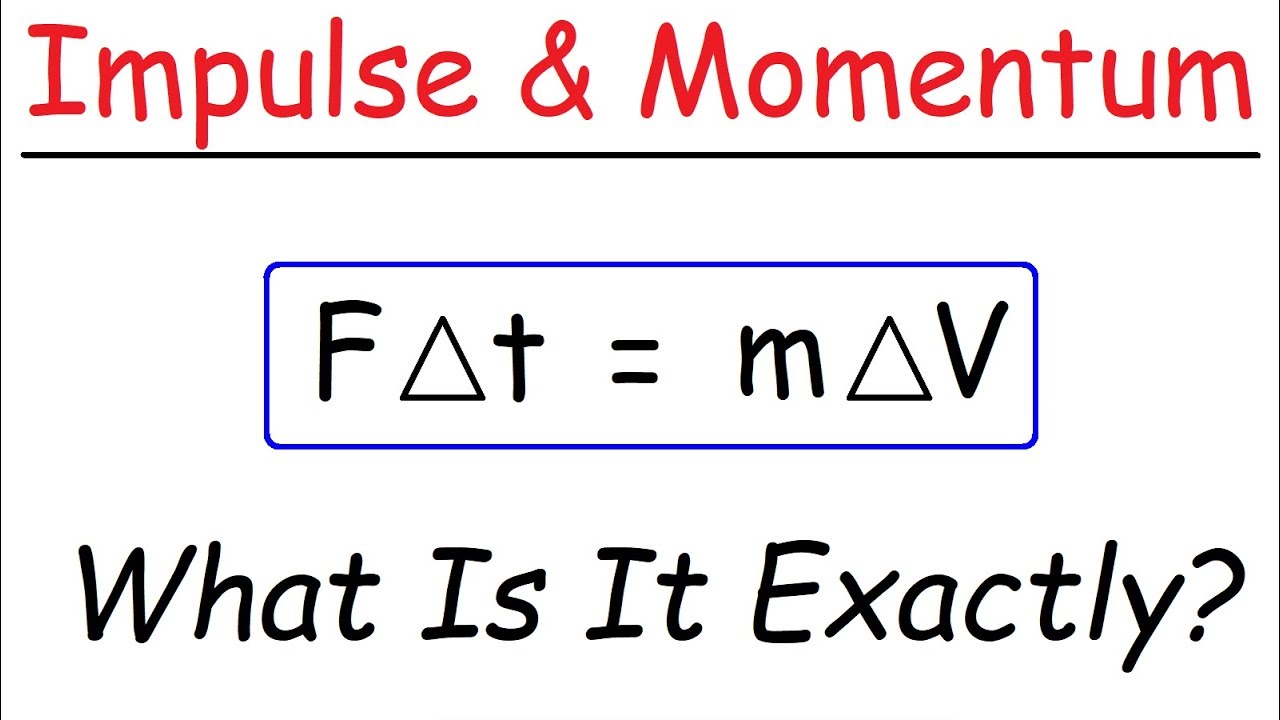
The impulse is the same ($10$ Ns), the change in momentum is the same ($10$ Ns) and so is the final speed ($10$ m/s). Now apply a force of $20$ N on the body for $\frac 1 2 $ seconds. However it does not reach that speed until one second after the froce was first applied. The impulse is $10 \times 1 = 10$ Ns and as this is equal to the change in momentum of the body the bodies final speed is $10$ m/s. Suppose a mass of $1$ kg, starting from rest, is subjected to a force of $10$ newtons for $1$ second. Now often it is the case that one is interested in what happens before and after a collision but one is not interested in what happens during the collision particularly if the time during which the collision occurs is much less than the times scale before and after the collision. As freecharly stated in his post, impulsive force is defined to be the force which acts for an infinitesimally short interval of time and yet is responsible for a finite change in momentum of the system on which the impulsive force is applied.Īs implied from Newton's Second Law of Motion, impulse is defined to be $$\textrm \Rightarrow \Delta p = F \Delta t$ ie it is something to do with change of momentum of a body.


 0 kommentar(er)
0 kommentar(er)
